베른하르트 리만
일단 리만 가설이라는 것을 알아봅시다.
리만 제타 추측은 리만 제타 함수의 모든 자명하지 않은 영점의 실수부가 1/2 이라는 추측이다.
아니 이게 무슨 말일까요...

먼저 '소수' 라는 개념을 알아야 합니다.
소수의 정의는 다음과 같습니다.
1과 자기 자신으로밖에 나누어 떨어지지 않고 자기 자신의 곱셈의 역수가 없는 수
아주 작은 소수는 찾기가 쉽지만, 큰 소수를 찾을려면 소인수 분해를 해야 합니다.
다들 중학교 수학이 기억이 안날 수 있어서, 복습하는 차원에서 적어봅니다.
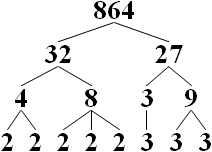
소인수 분해
소인수 분해란 1 보다 큰 자연수를 소인수(소수인 인수)들만의 곱으로 나타내는 것으로
가장 쉬운 방법은 작은 소수 부터 (2, 3, ...) 으로 부터 하나씩 나눠봐야 합니다.
위의 문단의 내용처럼 현대 컴퓨터에서는 소인수 분해를 빠르게 할 알고리즘이 없습니다.
예를 들어 193자리 수는 5개월간 30개의 2.2 GHz 옵테론 CPU를 동원하여 소인수분해가 되었습니다.
소인수분해의 난해함은 RSA와 같은 현대 암호의 핵심적 부분이 됩니다.
저희가 쓰는 이렇게 쓰는 인터넷도 전자상거래도 이 소수 기반의 보안 으로 이루어 진 것이죠.
그런 와중에 오일러라는 분이 소수를 가지고 곱했다 뺐다 했더니 원주율이 나오네? 라는 접근을 하게 되었습니다.
레온하르트 오일러
하지만 '오일러의 공식'으로 유명한 수학자 레온하르트 오일러(1707~1783)는 소수를 관찰하면서 소수로만 이뤄진 식을 하나 만들었다. 소수의 제곱을 소수의 제곱에서 1을 뺀 수로 나눈 뒤 끊임없이 곱하는 식(1번 식)을 정리했더니 '파이(원주율)'가 나타났다.
바로 이것이 '오일러의 공식' 으로 불리우는 유명한 발견 이었습니다.
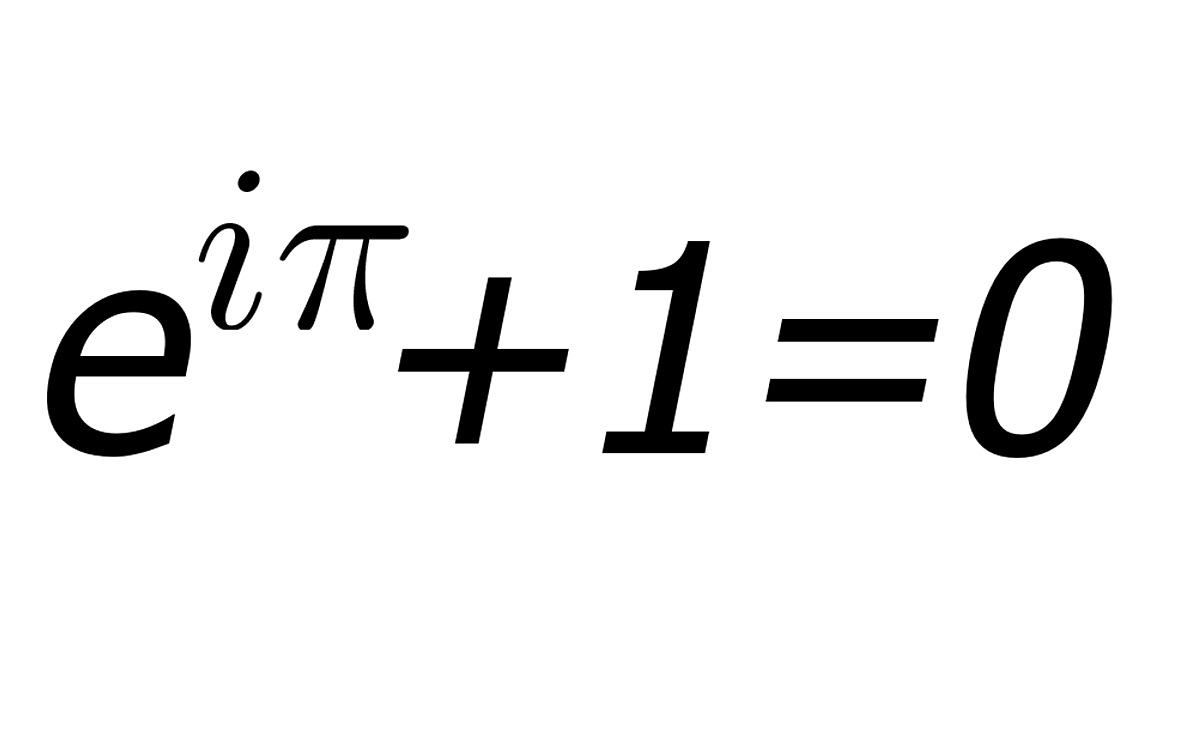
오일러의 공식

카를 프리드리히 가우스
당시 그의 나이 15살...
드디어 리만 가설의 주인공인 리만이 여기서 등장을 하게 됩니다.
사실 소수의 비밀을 못 알아낼지도 모릅니다.
다만 위의 오일러의 공식에서 돌출한 원주율 뿐만 아니라, 최근에는 양자물리학에서 쓰이던 공식이 리만 가설의 공식과 동일하다는 내용이 알려지면서... 단순히 수학자들의 놀이 일뿐이 아니라 자연의 숨겨진 비밀을 푸는 열쇠가 될지도 모른다는 생각을 하게 되었습니다.

ㅎㄷㄷ
그렇다면 혹시 패턴이 있다면 ai 가 소수의 패턴을 알 수 있지 않을까 라는 생각으로 접근하게 되었습니다.
왜냐고요?
그냥 무시하고 머신러닝 알고리즘을 훈련 시키려고 해도 입력한 데이터에 가까운 무언가만 가지게 될 것이며. 실제 예측이랑 터무니 없는 답만 나올 것이기 때문입니다.

face palm
Ref.