생각하는 중등수학 ②
음수는 왜 만들어졌을까?
우리는 지금 너무 자연스럽게 말한다.
“-3”, “영하 5도”, “잔고가 마이너스예요”
하지만 가만히 생각해보면 음수는 꽤 이상한 숫자다.
- 사과가 -3개 있을 수 있을까?
- 사람을 -2명 만날 수 있을까?
한때 수학에서도 음수는 존재하지 않는 숫자였다.
숫자는 원래 세는 도구였다
숫자는 아주 단순한 필요에서 시작했다.
- 양이 얼마나 되는지
- 몇 개가 있는지
- 얼마나 늘었는지
그래서 처음 숫자는 전부 양수였다.
- 양 3마리
- 곡식 10포대
- 사람 5명
👉 셀 수 있는 것만 숫자였다.
0조차도 늦게 등장했다
지금은 너무 당연한 0도 사실은 한참 뒤에 등장했다.
- 아무것도 없는 상태
- 기준점
- 시작점
0이 생기면서 숫자는 비로소 위치를 갖기 시작했다.
하지만 그럼에도 0보다 작은 숫자는 여전히 필요 없어 보였다.
문제가 생긴 순간
상황이 달라진 건 세는 것 말고, 비교하고 기록해야 할 때였다.
예를 들어 이런 상황이다.
- 돈을 빌렸다
- 물건을 덜 받았다
- 기준보다 아래로 내려갔다
“없다”로는 설명이 부족했다.
“3이 있는데, 5를 줘야 한다”
이 상황을 설명할 방법이 필요했다.
음수는 ‘부족함’을 기록하기 위해 등장했다
여기서 음수는 갑자기 하늘에서 떨어진 개념이 아니다.
이미 있는 기준에서 얼마나 부족한지를 표현하기 위한 도구
- 가진 돈보다 더 썼을 때
- 기준선보다 더 내려갔을 때
- 약속보다 모자랄 때
👉 음수는 **‘없는 것’이 아니라 ‘모자란 상태’**를 나타낸다.

숫자가 방향을 갖게 되다
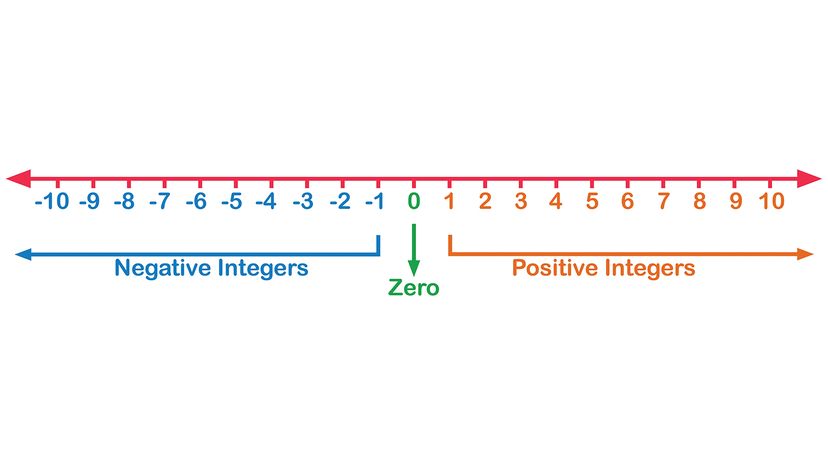
음수가 등장하면서 숫자는 단순한 개수가 아니라 방향을 가진 개념이 된다.
- 0을 기준으로
- 오른쪽은 양수
- 왼쪽은 음수
이때부터 숫자는 위치와 이동을 설명할 수 있게 된다.
- 앞으로 갔다
- 뒤로 물러났다
- 기준을 넘었다
이상하지만, 꼭 필요한 숫자
여전히 음수는 직관적이지 않다.
- 사과 -3개는 상상하기 어렵고
- 사람 -2명은 말이 안 된다
그런데도 우리는 음수를 쓴다.
왜냐하면 음수는 현실의 상태를 정확하게 기록해주기 때문이다.
생각하는 중등수학
이 글은 “음수는 이렇게 정의된다”라고 말하지 않는다.
대신 이런 질문을 남기고 싶다.
“숫자는 언제부터 단순한 개수가 아니게 되었을까?”
중등수학에는 이렇게 ‘필요해서 만들어진 개념’들이 많다.
- 0
- 음수
- 분수
- 문자
앞으로 이 시리즈에서는 그 필요의 순간을 하나씩 따라가 보려 한다.
정답보다, 생각이 오래 남는 방향으로.



다음 글 예고
생각하는 중등수학 ③ — 나머지는 실패한 계산일까?
딱 떨어지지 않는 계산이 왜 필요한지에 대해.