생각하는 중등수학 ⑭ — 함수는 왜 ‘기계’처럼 설명될까?

2026년 1월 30일

생각하는 중등수학 ⑭

함수를 처음 배울 때 이런 설명을 듣는다.

“x를 넣으면 y가 나온다.”

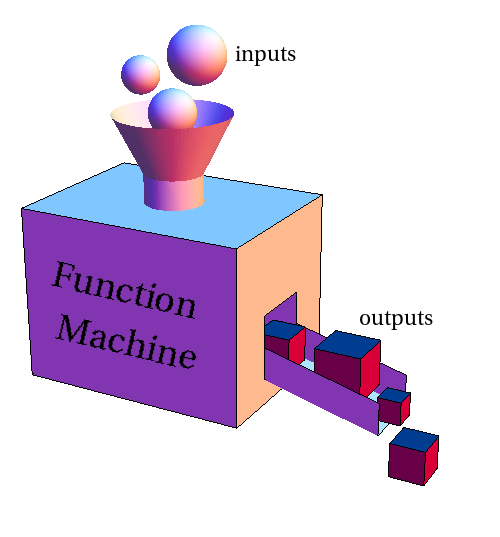
그리고 곧 이런 그림이 등장한다.

왜 함수는 사람이나 규칙이 아니라 기계처럼 설명될까?

수학이 다루는 대상이 점점 복잡해지면서 문제가 생겼다.

관계를 말로 설명하는 건 점점 어려워졌다.

그래서 수학은 관계를 단순한 약속으로 묶는다.

함수의 핵심은 아주 간단하다.

하나의 입력에 결과는 하나만 나온다

하지만 한 입력 → 하나의 출력 이 약속은 반드시 지켜진다.

기계로 설명하면 많은 게 쉬워진다.

함수는 과정보다 결과의 일관성을 중요하게 여긴다.

그래서 함수는 ‘블랙박스’처럼 다뤄진다.

기계에도 사용 설명서가 필요하듯, 함수에도 범위가 있다.

아무 값이나 넣으면 고장 나는 기계처럼, 함수도 허용된 범위가 있다.

함수를 단순 계산으로 보면 자꾸 헷갈린다.

함수는 이렇게 생각하면 좋다.

어떤 값이 들어오면 어떤 값이 대응되는가

이건 세부 구현일 뿐이다. 핵심은 대응 관계다.

함수의 등장은 수학의 시야를 넓혔다.

이제 수학은 값을 계산하는 학문에서 변화를 다루는 언어가 된다.

이 글은 함수 문제를 잘 푸는 법을 말하지 않는다.

대신 이런 질문을 남기고 싶다.

왜 수학은 관계를 설명할 때 ‘기계’라는 비유를 선택했을까?

함수는 사고를 단순화하기 위한 장치이지, 생각을 멈추게 하는 버튼이 아니다.

앞으로도 이 시리즈에서는 그 장치들이 왜 필요했는지를 천천히 따라가 보려 한다.

생각하는 중등수학 ⑮ — 함수의 그래프는 왜 그렇게 생겼을까?

식 하나가 왜 저 모양의 선이 되는지에 대해.