생각하는 중등수학 ⑬ — 그래프는 왜 직선부터 시작할까?

생각하는 중등수학 ⑬
그래프는 왜 직선부터 시작할까?
좌표를 배우고 나면 곧 그래프가 등장한다.
그리고 거의 예외 없이 첫 번째 그래프는 이렇다.
- 곡선이 아니라
- 복잡한 모양도 아닌
- 직선
왜 하필 직선일까?
직선은 가장 조용한 변화다
직선 그래프는 이렇게 말한다.
“한 칸 가면, 항상 똑같이 변한다.”
- x가 1 늘어나면
- y도 늘 같은 양만큼 변한다
이건 변화가 없는 게 아니라, 변화가 일정한 상태다.
변화가 일정하다는 건 무엇일까?
현실에서는 이런 상황이다.
- 매일 같은 속도로 걷는다
- 매 시간 같은 요금을 낸다
- 일정한 비율로 증가한다
이때 관계는 복잡하지 않다.
- 예측 가능하고
- 설명하기 쉽고
- 계산하기 편하다
그래서 수학은 이 상태를 기준으로 삼는다.
![]()
직선은 기준선이다
그래프에서 직선은 목표가 아니다.
기준이다.
- 여기서 벗어나면
- 얼마나 휘었는지
- 얼마나 빨라졌는지
- 얼마나 느려졌는지
모두 직선과 비교해서 말한다.
직선이 없으면 곡선도 설명할 수 없다.
기울기는 ‘변화의 크기’다
직선을 배우며 우리는 기울기를 만난다.
기울기는 이런 질문에 대한 답이다.
“얼마나 빠르게 변하는가?”
- 가파르면 빠르고
- 완만하면 느리다
기울기는 숫자로 표현된 변화의 감각이다.
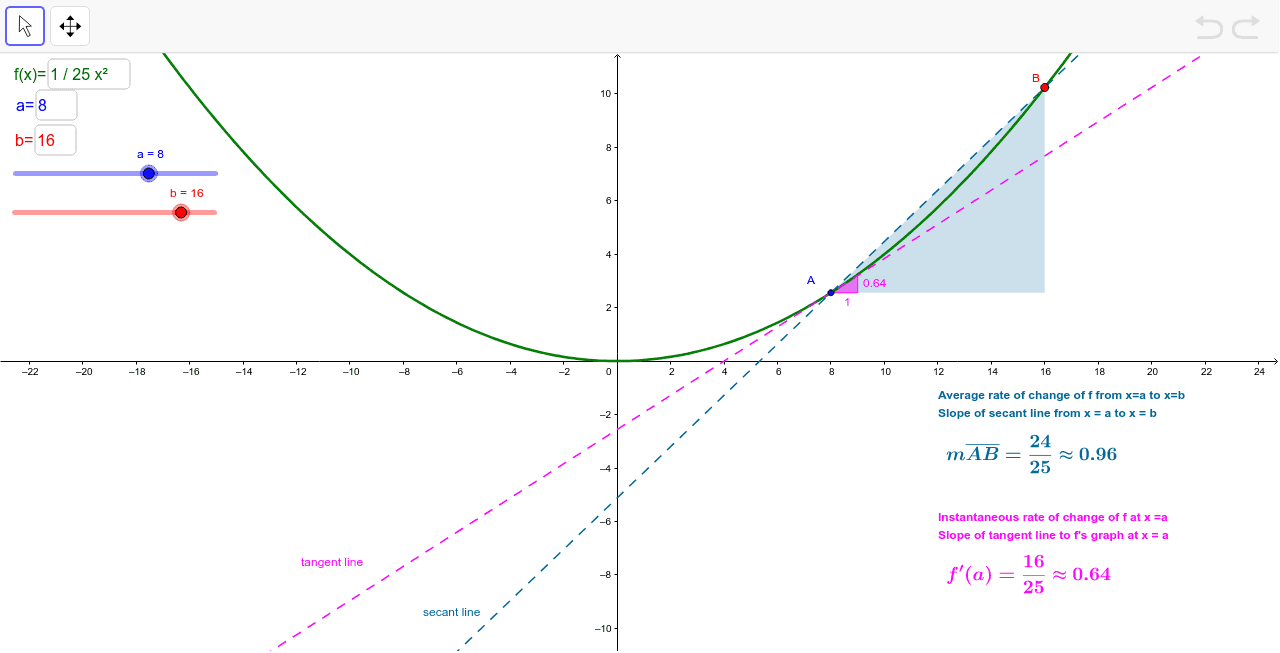
직선은 약속이 단순하다
직선은 수학적으로도 편하다.
- 식이 단순하고
- 계산이 반복 가능하고
- 오류가 적다
그래서 새로운 개념이 나올 때마다 수학은 이렇게 묻는다.
“이걸 직선으로 볼 수 있을까?”
직선으로 볼 수 있다면, 이해는 훨씬 쉬워진다.
하지만 현실은 대부분 곡선이다
아이러니하게도 현실의 변화는 대부분 직선이 아니다.
- 처음엔 느리다가
- 점점 빨라지고
- 다시 완만해진다
그래서 직선은 현실의 모습이 아니라 현실을 보기 위한 렌즈다.

생각하는 중등수학
이 글은 직선 그래프를 그리는 법을 말하지 않는다.
대신 이런 질문을 남기고 싶다.
왜 수학은 가장 단순한 변화부터 이해하려 했을까?
직선은 세상을 단순하게 만들기 위한 거짓말이 아니라, 복잡함을 견디기 위한 출발점이다.
앞으로도 이 시리즈에서는 그 출발점이 어떻게 확장되는지를 천천히 따라가 보려 한다.

다음 글 예고
생각하는 중등수학 ⑭ — 함수는 왜 ‘기계’처럼 설명될까?
입력과 출력이라는 말은 왜 수학에 들어왔을까?