생각하는 중등수학 ⑨ — 문자는 왜 숫자가 되었을까?

생각하는 중등수학 ⑨
문자는 왜 숫자가 되었을까?
수학을 하다 보면 어느 순간 이런 일이 벌어진다.
숫자 대신 x가 등장한다.
처음엔 낯설다.
- x는 숫자가 아닌데
- 값을 모르는 기호인데
- 왜 계산을 할 수 있을까?
숫자로는 부족해진 순간
초기의 수학은 대부분 숫자로 충분했다.
- 3개
- 10명
- 5번
하지만 문제는 상황이 조금만 복잡해질 때 생긴다.
“어떤 수에 3을 더하면 10이 된다.”
이 문장은 맞다. 하지만 계산할 수는 없다.
아직 숫자가 없기 때문이다.
‘모르는 것’을 그대로 두기
이때 수학은 의외의 선택을 한다.
모르는 걸 억지로 숫자로 만들지 말자.
대신 이렇게 말한다.
“이 값을 x라고 부르자.”
x는 답이 아니다. x는 자리를 표시한 기호다.
문자는 답이 아니라 약속이다
중요한 점은 이거다.
- x는 어떤 특정한 숫자가 아니다
- 대신 어떤 숫자든 될 수 있다
그래서 x는 숫자보다 더 많은 일을 한다.
- 여러 상황을 한 번에 다루고
- 조건을 일반화하고
- 같은 구조를 반복해서 쓰게 해준다
계산은 여전히 계산이다
문자가 등장해도 수학은 갑자기 달라지지 않는다.
- 더한다
- 뺀다
- 곱한다
- 나눈다
다만 대상이 숫자 하나에서 숫자의 자리로 바뀌었을 뿐이다.
그래서 우리는 문자로도 계산을 한다.
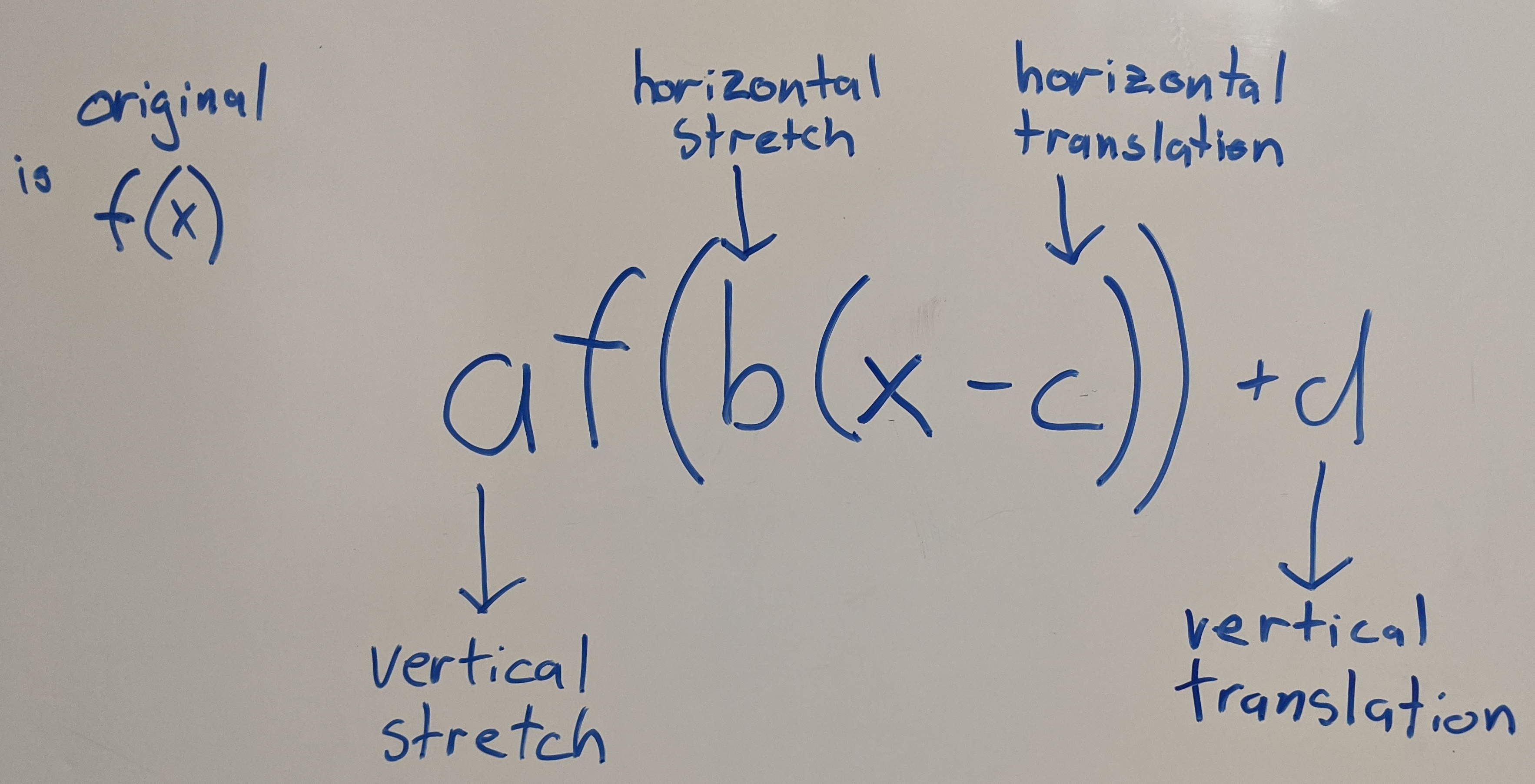
문자가 만든 가장 큰 변화
문자의 등장은 수학의 시선을 바꿨다.
- 하나의 문제 → 여러 문제
- 하나의 답 → 답의 구조
- 계산 → 관계
이때부터 수학은 결과보다 관계를 다루는 학문이 된다.
그래서 문자는 불편하다
문자는 직관적이지 않다.
- 손에 잡히지 않고
- 값이 보이지 않고
- 당장 답을 주지 않는다
그래서 많은 사람이 문자가 나오면 수학이 어렵다고 느낀다.
하지만 그 불편함 덕분에 수학은 더 멀리 갈 수 있었다.

생각하는 중등수학
이 글은 문자 계산을 잘하는 법을 말하지 않는다.
대신 이런 질문을 남기고 싶다.
왜 수학은 굳이 답을 미루는 방식을 선택했을까?
문자는 답을 숨기기 위한 장치가 아니라, 생각을 확장하기 위한 공간이다.
앞으로도 이 시리즈에서는 그 공간이 왜 필요했는지를 하나씩 따라가 보려 한다.

다음 글 예고
생각하는 중등수학 ⑩ — 방정식은 왜 ‘균형’일까?
등호는 왜 항상 가운데에 서 있을까?